飛行機はなぜ飛べるのか
揚力はなぜ発生するのか
その1
飛行機は翼が作る揚力と呼ばれる力で空へ上昇することができる。揚力はなぜ発生するのか。そしてジャンボジェットのような大きな飛行機を持ち上げる力はどこから得られているのか。多くの人が飛行機に関して抱く最初の疑問点であろう。いろいろ説明がなされているが、次のようなものを見た方も多いと思う。
「飛行機の翼の断面(翼型という)は図1のように上に反った形状をなしている。翼型に当たった流れは、上面と下面に分かれる。上面は大きな反りがあるので、下面をよりも翼後端までの距離が長い。翼後端で上下の流れが一致するには、上面の流れは下面の流れよりも速くなくてはならない。速い流れの圧力はベルヌーイの法則によって低くなる。上面の圧力が下面の圧力よりも低いので、翼は上に持ち上げられる。」。
図1 間違った揚力の説明
巧妙な説明だが、残念ながら間違っているところがある。「ベルヌーイの定理」とは、流速と圧力の関係を決める重要な定理である。それ自体に誤りがあるのではない。問題は、「翼後端で上下の流れが同時に再会する」というところである。同時に合流しなくてはならない理由はどこにもない。風洞で流れの様子を観察すると、上面の流れは下面の流れよりも速く流れさってしまうのが分かる。
そもそも空気の存在を正しく認識するのは難しい。「空」とは地面の上の何もない所という意味だから、「空虚」「空白」などと「空」は何もないことに使われている。だが、実際には重さが存在する。空気の重さに関してクイズを出してみよう。
「問題1:1メートル立方の空気の重さはどれに近いか?」
1.1円玉ひとつ
2.鉛筆1本
3.水の入ったペットボトル1本
答えは3、およそ1.2kgである。そんなに重いのかと思ったかたも多いのではないか。そんな重さを感じないのか。それは、我々が空気のなかで生活しているからである。ちょうど水中で水の重さを感じ難いようにである。ビンに水を詰めると重くなる。ところが水中にそのビンを入れると重さを感じない。それはビンに浮力が働くからである。これは「アルキメデスの原理」である。物体が流体中で排除した流体の重さだけ浮力を受ける、というものだ。空中でも同じように浮力が働く。空中で空気の重さを感じないのはそのためだ。
水中で水の重さを感じるとしたら、それは、水中を動く時、または、流れる水中にいる時である。水の重さは1立方メートルあたり1トンである。水流の勢いは洪水の例を見るまでもなく凄まじい。空気は軽いとはいえ、1立方メートルあたり約1キログラムあるからそれが流れると、つまり風がおきると大きな力を受ける。
これは簡単に実験できる。大きなビニールのゴミ袋に空気を詰めてみよう。浮力が働くのでゴミ袋は空気を詰めても重くはない。ところが、空気は1リットルあたり約1グラムの重さがある。だから、空気を詰めた大きなゴミ袋をぶつけるとそこそこの衝撃となる。
走行中の車の窓から手を出し、手のひらを水平から少し傾けると気流の圧力を受け、少し上に持ちあげられる。重さのある空気がぶつかった反作用である。この力が揚力の要因であるとする説明に出会うことがある。流れに傾けて板のような物体をおけば確かに反作用で上向きの力が発生する。ただ、その力は揚力に比べるとずっと小さい。
流れがぶつかった際に発生する反作用で力が発生することを最初に数学的に説明したのはアイザック・ニュートンであった。ニュートンは図2のように、空気(一般には流体)を小さな粒子の集まりと考え、その粒子が物体にあたることで力を及ぼすと考えた。流体の速度をVとし、流体の密度をローとし、物体を面積Sの円盤としよう。一秒間に物体に衝突する流体の質量は空気密度と速度と円盤の面積の積であり、衝突によって速度が0になるとすると、1秒間における運動量はさらに速度を掛けた大きさになる。単位時間当たりの運動量の変化が物体に作用する力となるので、物体には図2のような力が加わる。これは流体が空気の場合には、空気抵抗となる。
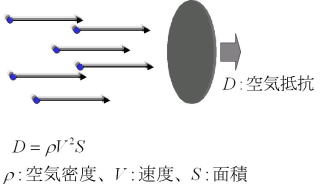
図2 ニュートンの考えた流体力の計算法
空気抵抗が流速の2乗に比例し、物体の面積にも比例するという結果は定性的には正しい。ニュートンは1687年に、大きさの異なる球をセントポール寺院のドームから落として大きさによる抵抗の違いを確認したという。物体の落下速度は物体の質量にはよらず一定であるという、ガリレオの主張が崩されたのだ。物体の形や大きさが変われば、空気抵抗が変化するので、実際には、落下速度も変化するのが正しい解釈である。
流れに置かれた板が傾きを持てば、衝撃力は板に垂直に作用する。流れに垂直な力を揚力、平行な力を抵抗と定義するから、確かに揚力が発生することになる。ニュートンの時代に、飛行機を研究した人はいなかっただろうから、ニュートンの理論で飛行機が設計されることもなかった。ニュートンの示した流体抵抗の算出方法は、当時の軍艦の設計には、役立ったと思われる。ただし、ニュートンがこの理論を構築したのは、宇宙の惑星の運動を解析するためであった。当時、宇宙は均質な物質で満たされていると考えられていた。ニュートンは万有引力の法則によって惑星の運動が説明できることを示した。惑星の運動が力学法則に支配されていることを明らかにしたのだ。ただし、宇宙が流体物質に満たされているとすると、抵抗が生じ、時間がたつと全ての惑星は太陽に吸い寄せられてしまう。そうはなっていないことから、宇宙は真空であるとニュートンは主張した。
次回に続く
鈴木真二(東京大学航空宇宙工学専攻)
|

